
Dalam serangkaian tata letak aturan, tidak ada satu 'peluru perak' yang merupakan obat untuk semua kesulitan perhitungan. Masalah yang berbeda membutuhkan penggunaan berbagai jenis proses. Seorang programmer yang sangat baik menggunakan banyak taktik ini berdasarkan jenis hambatan. Di weblog ini memasang, saya akan membahas 2 konsep desain algoritma fundamental:
Algoritma serakah
Algoritma serakah, seperti namanya,secara konsisten membuat pilihan yang tampaknya paling sederhana pada detik itu. Pendekatan yang membuat keputusan optimal regional dalam keinginan bahwa resolusi ini akan menghasilkan resolusi optimal secara global.
Bagaimana Anda memutuskan pilihan mana yang optimal?
Asumsikan bahwa Anda memilikifungsi beroperasiItu perlu dioptimalkan (baik dimaksimalkan atau diminimalkan) pada aspek tertentu. Algoritma serakah membuat pilihan serakah pada setiap langkah untuk memastikan bahwa tujuan beroperasi dioptimalkan. Algoritma serakah memiliki murni satu bidikan untuk menghitung solusi optimal agar ituitu tidak pernah berjalan lagi dan membalikkan keputusan.
Algoritma serakah memiliki beberapa manfaat dan kelemahan:
- Ini jelas sekalimemberi Anda algoritma serakah(Atau mungkin beberapa algoritma serakah) untuk kekurangan.
- Menganalisis waktu berjalan untuk algoritma serakah akan berkali -kali menjadi jauh lebih sederhanadaripada untuk taktik yang berbeda (seperti membagi dan mengatasinya).Untuk teknik Divide and Conquer, tidak bersih apakah metode ini cepat atau lamban.Ini karena pada masing-masing derajat rekursi ukuran semakin kecil dan jumlah sub-difikulties meningkat.
- Bagian yang sulit adalah bahwa untuk algoritma serakahAnda perlu bekerja lebih keras untuk memahami masalah kebenaran.Bahkan dengan algoritma yang ideal, itu sulit untuk menunjukkan mengapa ini benar.Membuktikan bahwa algoritma serakah yang benar adalah ekstra dari seni daripada sains.Ini mensyaratkan sejumlah kreativitas.

Mari kita menyeberang beberapa masalah optimasi terkenal yang menggunakan proses desain algoritmik serakah:
Dalam masalah ini, input kami adalah serangkaian durasi waktu dan output kami adalah subset dari interval yang tidak tumpang tindih. Tujuan kami adalah untuk memaksimalkan jumlah interval yang dipilih dalam tubuh-waktu tertentu. Secara formal SpeakMe, kami memiliki serangkaian permintaan 1, 2,. . . , n;Permintaan i-th sesuai dengan periode waktu yang dimulai pada s (i) dan menyelesaikan pada f (i). Subset dari permintaan adalahsesuaiJika tidak ada dari mereka yang tumpang tindih dalam waktu, dan tujuan kami adalah menerima subset sebesar yang dapat dicapai
Unit yang kompatibel dengan panjang maksimum akan disebut sebagai<strong>optimal</strong>. Dengan menggunakan kebingungan ini, kami akan membuat diskusi kami tentang algoritma serakah jauh lebih banyak beton. Gagasan utama dalam algoritma serakah untuk penjadwalan interval adalah dengan menggunakan aturan lurus ke depan untuk memilih permintaan pertama I_1. Setelah permintaan I_1 disetujui, kami menolak semua permintaan yang tidak sesuai dengan I_1. Kami kemudian memilih permintaan I_2 berikutnya untuk diterima dan sekali lagi menolak semua permintaan yang tidak sesuai dengan I_2. Kami melanjutkan selama mode ini sampai akhirnya kami kehabisan permintaan.
Aturan serakah yang menghasilkan solusi optimal didasarkan pada konsep ini: kita harus menerima pertama permintaan yang selesai terlebih dahulu, itu adalah permintaan yang saya (i) sekecil yang dapat dicapai. Ini juga terasa pemikiran herbal: kami memastikan bahwa sumber daya kami akan menjadi tidak terikat secepat yang dapat dicapai sementara tetap menyenangkan satu permintaan. Dalam metode ini, kami akan memaksimalkan waktu yang tersisa untuk memenuhi permintaan lain. Secara formal, kami akan menggunakan R untuk menunjukkan serangkaian permintaan yang kami tidak wajib atau tolak tetapi, dan gunakan A untuk menunjukkan serangkaian permintaan yang diterima.
1 - Initially allow R be the set of all requests, and permit A be empty2 - While R is now not yet empty:3 - Choose a request i in R that has the smallest finishing time4 - Add request i to A5 - Delete all requests from R which are not compatible with request i6 - EndWhile7 - Return the set A as the set of accepted requestsInilah contoh cara algoritma berjalan. Pada setiap satu langkah, interval yang dipilih adalah garis hitam, dan interval yang dihapus pada langkah yang sesuai ditunjukkan dengan garis putus-putus.

Kita bisa membuat algoritma kita berjalan dalam waktu o (n logn) sebagai berikut:
- Kami mulai melalui menyortir permintaan N sehingga untuk menyelesaikan waktu dan memberi label dalam urutan ini;Artinya, kita dapat mengharapkan bahwa f (i) <= f (j) sementara saya <j.Ini membutuhkan waktu O (n Logn).
- Dalam waktu tambahan O (n), kami mengumpulkan array [1 ... n] dengan perkebunan yang s [i] mencakup signifikansi S (i).
- Kami sekarang memilih permintaan dengan memproses interval dalam urutan peningkatan f (i).Kami secara konsisten memilih interval pertama;Kami kemudian mengulangi interval secara berurutan sampai akhirnya mencapai interval pertama j yang s (j)> = f (l);Kami kemudian memilih yang ini dengan baik.
- Lebih normal, jika interval terbaru yang kami pilih berakhir pada waktu f, kami terus berulang dengan interval berikutnya sampai pada akhirnya kami mencapai 1 J yang s (j)> = f.Dalam metode ini, kami mengimplementasikan algoritma serakah yang dianalisis di atas dalam satu pass tunggal melalui interval, menghabiskan waktu reguler selangkah dengan interval.Dengan demikian, bagian algoritma ini membutuhkan waktu O (n).
Dalam hambatan ini, input kami adalah kumpulan interval waktu dan output kami adalah partisi dari interval, setiap bagian dari partisi terdiri dari interval yang tidak tumpang tindih. Tujuan kami adalah untuk mengurangi jumlah komponen di partisi. Sistem serakah adalah untuk memikirkan interval dalam memperluas urutan waktu dimulai dan kemudian menugaskannya ke bagian yang kompatibel
Sebagai ilustrasi masalah ini, pertimbangkan kesempatan sampel di simbol lebih rendah dari (baris utama). Permintaan dalam contoh ini semua dapat dijadwalkan menggunakan 3 aset, seperti yang ditunjukkan pada baris terendah-di mana permintaan diatur ulang menjadi 3 baris, setiap yang berisi satu set interval yang tidak tumpang tindih: baris pertama terdiri dari masing-masing interval yang ditetapkanKe sumber pertama, baris kedua berisi semua yang ditugaskan ke sumber momen, dan sebagainya.
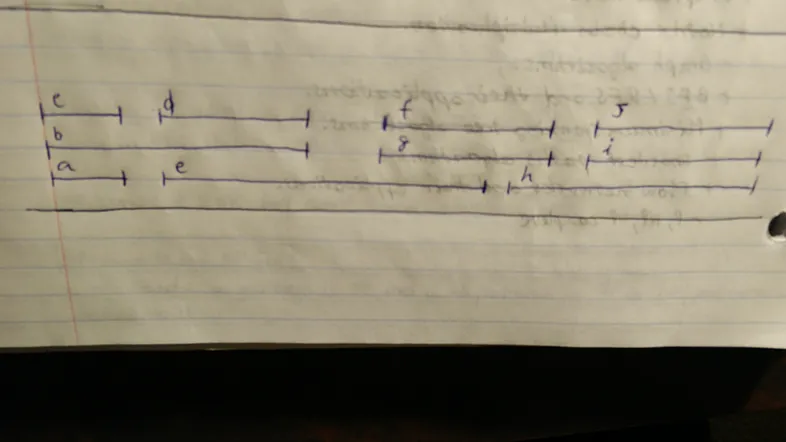
Misalkan kita mendefinisikankedalamandari satu set interval menjadi jumlah terbesar yang melewati elemen yang belum menikah pada timeline. Kemudian, kita dapat menyatakan bahwa selama contoh partisi interval apa pun, berbagai sumber daya yang dianggap perlu tidak kurang dari kedalaman serangkaian interval. Dengan demikian kita dapat merancang algoritma serakah sederhana yang menjadwalkan semua interval menggunakan banyak sumber daya yang sama dengan kedalaman. Ini segera menyiratkan optimalitas algoritma, karena tidak ada solusi yang dapat menggunakan beberapa aset yang lebih kecil dari kedalaman.
Misalkan D menjadi kedalaman himpunan interval;Kami menunjukkan cara menetapkan alabelUntuk setiap interval, tempat label berasal dari set angka 1, 2,. . . , D, dan tantangan memiliki barang-barang berharga yang tumpang tindih interval dan dikategorikan dengan angka unik
Ini menawarkan solusi yang disukai, melihat bahwa kita dapat menafsirkan setiap angka sebagai nama sumber daya, dan label dari setiap interval sebagai identifikasi sumber daya yang ditetapkannya. Algoritma yang kami gunakan untuk itu adalah metode serakah one-flow langsung yang memerintahkan interval dengan acara awal mereka. Kami menjalani interval dalam urutan ini, dan mencoba untuk menetapkan untuk setiap interval kami menemukan label yang belum ditugaskan ke interval sebelumnya yang tumpang tindih. Secara khusus, kami memiliki deskripsi selanjutnya:
1 - Sort the intervals by their begin instances, breaking ties arbitrarily.2 - Let I_1, I_2, ..., I_n denote the intervals in this order.3 - For j = 1, 2, 3, ..., n:4 - For each one interval I_i that precedes I_j in sorted order and overlaps it:5 - Exclude the label of I_i from consideration for I_j6 - Endfor7 - If there is any label from [1, 2, ..., d] that has not been excluded then:eight - Assign a non-excluded label to I_j9 - Else:10 - Leave I_j unlabeled11 - Endif12 - EndforJika kita menggunakan algoritma serakah di atas, setiap interval akan diberi label, dan no 2 interval tumpang tindih akan memperoleh label yang sama. Algoritma serakah di atas menjadwalkan setiap interval pada sumber daya, menggunakan banyak sumber daya yang sama dengan kedalaman himpunan interval. Ini adalah jumlah sumber daya yang optimal yang diperlukan.
Pemrograman Dinamis
Katakanlah kami memiliki sistem, dan untuk menentukan keadaannya pada waktuT, kami memiliki jumlah tertentu yang disebut negara bagianvariabel. Akan ada saat-saat ketika kita memutuskan mana yang berdampak pada keadaan mesin, yang mungkin atau mungkin tidak dianggap sebagai kita sebelumnya. Keputusan atau modifikasi ini sama dengan perubahan variabel negara. Hasil dari pilihan yang sudah ketinggalan zaman membantu kita dalam memilih yang takdir.
Apa yang bisa kita selesaikan dari ini? Akan lebih sederhana untuk mengatakan dengan tepat apa yang menjadi ciri khasDynamic Programming (DP)Setelah kami mempertimbangkannya dalam aksi, tetapi ide utama diambil dari naluri di belakang perpecahan dan menaklukkan dan sebagian besar adalah yang lain dari proses serakah. Kita perlu mengganggu masalah menjadi serangkaian sub-masalah yang tumpang tindih, dan meningkatkan perawatan ke sub-difikulti yang lebih besar dan lebih besar. Jika Anda diberi masalah, yang dapat rusak menjadi sub-masalah yang lebih kecil, dan sub-masalah yang lebih kecil ini masih dapat dipecah menjadi yang lebih kecil-dan jika Anda memanipulasi untuk mengetahui bahwa ada beberapa sub-masalah yang tumpang tindih, maka Andapasti mengalami masalah DP
Konsep tengahnya adalah untuk menghindari pekerjaan yang berulang dengan mengingat hasil parsial dan konsep ini mengungkapkan kegunaannya dalam banyak situasi keberadaan nyata. Dalam pemrograman, pemrograman dinamis adalah teknik yang kuat yang memungkinkan seseorang untuk menjernihkan berbagai jenis masalah dalam waktu o (n²) atau o (n³) di mana pendekatan naif mungkin membutuhkan waktu eksponensial.
Di satu sisi, karena itu kita dapat melihat DP sebagai berjalan dekat dengan ambang batas pencarian brute-force: meskipun secara sistematis beroperasi oleh serangkaian perawatan yang layak secara eksponensial untuk masalah ini, ia melakukan ini tanpa pernah menganalisis semuanya secara eksplisit. Sebagai hasil dari tindakan penyeimbangan yang hati-hati inilah DP bisa menjadi cara yang sulit untuk terbiasa;Biasanya membutuhkan banyak latihan yang masuk akal di masa lalu yang benar-benar nyaman dengan itu.
Mari kita membahas tentang masalah optimasi terkenal yang menggunakan pendekatan desain algoritmik pemrograman dinamis:
Kami telah melihat bahwa algoritma serakah yang dipilih menghasilkan solusi optimal untuk krisis penjadwalan interval dasar, di mana tujuannya adalah untuk menerima serangkaian interval non-tumpang tindih yang baik. Masalah penjadwalan interval tertimbang adalah versi yang lebih luas, di mana setiap interval memiliki bobot tertentu, dan kami ingin menerima satu set bobot terbesar. Input adalah seperangkat interval waktu, di mana setiap interval memiliki bobot. Output adalah subset dari interval yang tidak tumpang tindih. Tujuan kami adalah untuk memaksimalkan jumlah bobot dalam subset. Sistem rekursif lurus ke depan dapat dianggap lebih rendah dari:
Weighted-Scheduling-Attempt ((s_1, f_1, c_1), …, (s_n, f_n, c_n)):1 - Sort intervals by their finish time.2 - Return Weighted-Scheduling-Recursive (n)Weighted-Scheduling-Recursive (j):1 - If (j = zero) then Return 02 - okay = j3 - While (interval k and j overlap) do k—-four - Return max(c_j + Weighted-Scheduling-Recursive (k), Weighted-Scheduling-Recursive (j - 1))Pikirannya adalah untuk menemukan interval baru-baru ini sebelumnya interval yang ada (dalam array yang diurutkan) yang tidak tumpang tindih dengan interval saat ini ARR [J-1]. Setelah kami menemukan interval seperti itu, kami berulang untuk semua interval sampai interval itu dan menambah bobot interval yang ada pada hasilnya. Meskipun sistem ini berfungsi, gagal secara spektakuler karena sub-masalah yang berlebihan, yang menghasilkan waktu jogging eksponensial
Untuk meningkatkan kompleksitas waktu, kita dapat berusaha keras metode pemrograman dinamis top-down<strong>memoisasi. </strong>Kita bisa menyimpan pentingnya<strong>Rekursif Jadwal Berat</strong>Di lokasi yang praktis secara global pertama kali kami menghitungnya dan kemudian dengan tulus menggunakan nilai yang telah dikomputasi ini dalam preferensi untuk semua panggilan rekursif di masa depan. <strong> </strong>Di bawah ini Anda bisa melihat pseudocode O (n²) untuk metode ini:
Weighted-Sched ((s_1, f_1, c_1), …, (s_n, f_n, c_n)):1 - Sort intervals by their conclude time.2 - Define S[0] = 03 - For j = 1 to n do:four - k = j5 - While (intervals k and j overlap) do k—-6 - S[j] = max(S[j - 1], c_j + S[k])7 - Return S[n]Contoh pelaksanaanBerbobot berbobotdigambarkan dalam simbol di bawah. Di setiap generasi, algoritma mengisi satu entri tambahan array S, dengan membandingkan signifikansi C_J + S [k] dengan signifikansi S [j-1]. Di sini, K adalah indeks terbesar dari interval C_J dan tidak akan tumpang tindih dengan j.
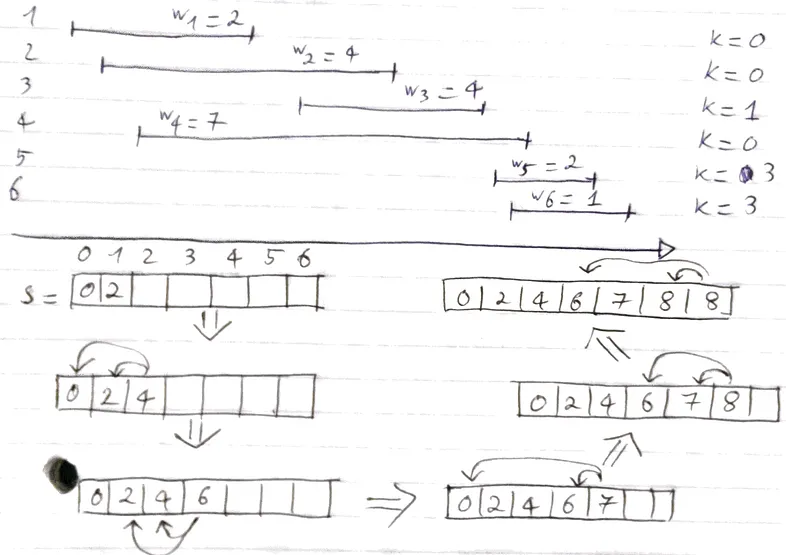
Untuk hambatan ini diberikan input sebagai rantai angka, kami berharap output dari peningkatan selanjutnya. Tujuan kami adalah untuk memaksimalkan ukuran setelahnya. Menggunakan pemrograman dinamis lagi, algoritma O (n²) mengikuti:
Longest-Incr-Subseq(a_1, …, a_n):1 - For j = 1 to n do:2 - S[j] = thirteen - For k = 1 to j - 1 do:4 - If a_k < a_j and S[j] < S[k] + 1 then:5 - S[j] = S[k] + sixteen - Return max_j S[j]Contoh pelaksanaanSubseq Incr terpanjangdigambarkan dalam simbol kurang dari. Dalam setiap iterasi, s [j] adalah panjang terbesar dari peningkatan yang meluas dari angka J pertama yang diselesaikan dengan angka J-th. Perhatikan bahwa s [j] = 1 + maksimum s [k] di mana k <j dan a_k <a_j.

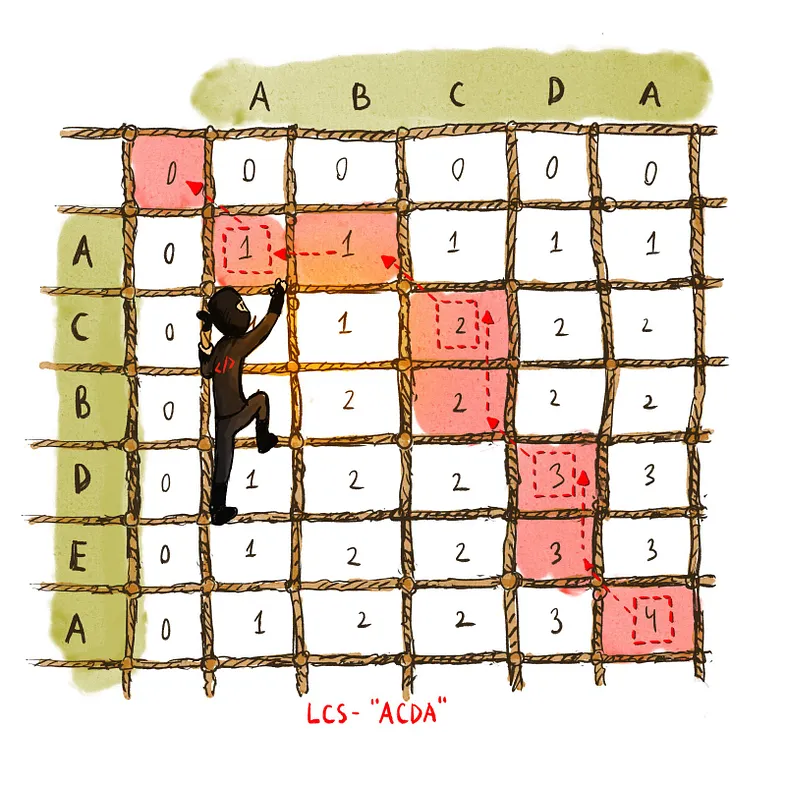
Diberikan 2 urutan, temukan panjang yang paling lama terjadi di keduanya. Selanjutnya dalam konteks ini adalah seri yang muncul dalam urutan relatif yang sama, namun tidak harus berdekatan. Misalnya, "ABC", "ABG", "BDF", "AEG", "ACEFG", dll. . . Adalah setelah "ABCDEFG. "Jadi serangkaian panjang n memiliki 2^n unik yang dapat dibayangkan. Misalnya, rata-rata terpanjang setelah urutan input "ABCDGH" dan "AEDFHR" adalah "ADH" dengan panjang 3. Menggunakan pemrograman dinamis lagi, algoritma O (m x n) terbukti di bawah ini, di mana m adalah panjang dari urutan pertama dann adalah panjang urutan momen:
Longest-Common-Subseq(u, v):1 - Initialize S[j, k] to 0 for each j = 0, ..., m and every k = 0, ..., n2 - For j = 1 to m do:3 - For k = 1 to n do:4 - S[j, k] = max(S[j - 1, k], S[j, k - 1])5 - If (u[j] = v[k]) then:6 - S[j, k] = S[j - 1. k - 1] + 17 - Return S[m, n]Dalam setiap iterasi, s [j, k] adalah yang paling panjang dari u_1,…, u_j dan v_1,…, v_k. Perhatikan bahwa:
- S [j, k] = 1 + S [j - 1, k - 1] Jika j> 0 dan u_j = v_k.
- S [j, k] = maks (s [j - 1, k], s [j, k - 1]) Jika j> 0 dan u_j! = V_k (ini dengan alasan yang tidak dapat kita gunakan sama -sama u_jdan v_k dalam rata -rata input, jadi kita harus melewati setidaknya satu dalam semuanya).
Mengingat bobot dan nilai item N, kami ingin memposisikan hal-hal ini dalam ransel kemampuan W untuk mendapatkan signifikansi keseluruhan maksimum di Knapsack. Dengan kata lain, diberi dua array integer val [0,. . . , n-1] dan wt [0,. . . , n-1] yang mewakili nilai dan bobot yang terkait dengan masing-masing produk N dan integer W yang mewakili kemampuan ransel, kami inginkanUntuk menemukan subset kepentingan maksimum val [] sedemikian rupa sehingga jumlah bobot subset ini lebih kecil dari atau sama dengan W. Kita tidak dapat menghancurkan barang dagangan, baik memilih seluruh barang dagangan, atau tidak mengikutinya (karenanya (karenanyaproperti 0–1). Di bawah ini adalah solusi pseudocode pemrograman dinamis O (n x w):
Knapsack-Indivisible(n, c, w, W):1 - Initialize S[0, v] = 0 for each v = 0, …, W2 - Initialize S[k, 0] = 0 for every k = 0, …, n3 - For v = 1 to W do:4 - For k = 1 to n do:5 - S[k, v] = S[k - 1, v]6 - If (w_k <= v) and (S[k - 1, v - w_k] + c_k > S[k, v]) then:7 - S[k, v] = S[k - 1, v - w_k] + c_k8 - Return S[n, W]Dalam setiap iterasi, s [k, v] adalah nilai maksimum dari subset item yang dipilih dari item k pertama di mana bobot subset kurang dari v. Perhatikan bahwa:
- S [k, v] = 0 jika k = 0 atau v = 0.
- S [k, v] = maks (s [k - 1, v], c_k + s [k - 1, v - w_k]) jika k> 0 dan v> 0.
Diberi urutan matriks, temukan terima kasih paling hijau untuk melipatgandakan matriks ini bersama-sama. Masalahnya tidak jelas untuk melakukan perkalian, tetapi hanya untuk menentukan urutan mana untuk melakukan perkalian. Kami memiliki banyak opsi untuk melipatgandakan rantai matriks mengingat fakta bahwa multiplikasi matriks bersifat asosiatif. Dengan kata lain, tidak peduli bagaimana kita membagi produk, hasilnya mungkin serupa. Misalnya, jika kami memiliki empat matriks A, B, C, dan D, kami memiliki: (ABC) D = (AB) (CD) = A (BCD) =…. Solusi pemrograman dinamis dapat diamati di bawah ini:
Matrix-Chain-Multiplication(a_1, …, a_n):1 - For L = 1 to n do S[L, L] = 02 - For d = 1 to n do:3 - For L = 1 to n - d do:4 - R = L + d5 - S[L, R] = Infinity6 - For k = L to R - 1 do:7 - tmp = S[L, k] + S[k + 1, R] + a_(L - 1) x a_K x a_R8 - If S[L, R] > tmp then: S[L, R] = tmp9 - Return S[1, n]Dalam setiap iterasi, S [l, r] adalah jumlah minimum langkah yang diperlukan untuk mengalikan matriks dari l-th ke r-th (a_l x a_ (l + 1) x. . . X a_ (r-1) x a_r). Perhatikan bahwa:
- S [l, r] = 0 jika l = R.
- S [l, r] = min (s [l, k] + s [k + 1, r] + a_ (l - 1) x a_k x a_r).
Perbandingan
Kita dapat membuat beberapa hal tekad tampak paling sederhana dalam waktu intervensi dan kemudian menyelesaikan subproblem yang bangun nanti. Keputusan yang dibuat oleh algoritma serakah mungkin bergantung pada opsi yang dibuat sejauh ini tetapi tidak pada pilihan masa depan atau semua opsi untuk subproblem. Ini secara iteratif membuat satu resolusi serakah setelah beberapa yang lain, mengurangi setiap kesulitan yang diberikan menjadi yang lebih kecil. Dengan kata lain, algoritma serakah karena tidak ada akun yang mempertimbangkan kembali opsinya.
Ini adalah perbedaan utama dari pemrograman dinamis, yang lengkap dan dijamin menemukan jawabannya. Setelah setiap derajat, pemrograman dinamis membuat pilihan berdasarkan semua pilihan yang dibuat pada tahap sebelumnya, dan dapat memikirkan kembali jejak algoritmik tahap yang sudah ketinggalan zaman ke solusi.
Misalnya, katakanlah bahwa Anda harus mendapatkan dari titik A untuk menunjukkan B secepat dapat dicapai, dalam metropolis tertentu, selama jam sibuk. Algoritma pemrograman yang dinamis akan memeriksa catatan lalu lintas lengkap, melihat ke semua campuran jalan yang dapat Anda ambil, dan murni kemudian memberi tahu Anda yang mana dari mereka yang paling cepat. Rute, Anda bisa menunggu sebentar sampai algoritma selesai, dan pada dasarnya dapat Anda mulai menggunakan. Jejak yang akan sering Anda ambil adalah yang tercepat (dengan asumsi bahwa tidak ada yang dimodifikasi di lingkungan luar).
Di sebelah tangan yang berlawanan, algoritma serakah akan mulai Anda berkendara langsung dan akan memilih jalan yang muncul paling cepat di setiap persimpangan. Seperti yang Anda pertimbangkan, proses ini mungkin tidak menghasilkan waktu kedatangan tercepat, karena Anda dapat mengambil beberapa jalan "mudah" dan kemudian mendapati diri Anda terjebak dalam kemacetan lalu lintas.
---
Jika Anda benar-benar ingin mematuhi pekerjaan saya pada ilmu komputer dan sistem cerdas, Anda dapat melihat sayaSedangDanGitHub, selain inisiatif lain di https://jameskle. com/. Anda juga dapat men-tweet saya diTwitter,E-mail saya segera, atauTemukan saya di LinkedIn. AtauJadilah bagian dari milis sayat Untuk mendapatkan pemikiran terbaru saya tepat di kotak masuk Anda!